Projet IHM - Les entrelacs celtes

Objectif : réalisation d'une application de construction d'entrelacs celtes.

Les noeuds et entrelacs remontent à la civilisation celte qui, déjà au IV^e siècle avant notre ère, sculptait des motifs d'entrelacs sur ses menhirs dressés. Un entrelacs est composé de différents noeuds entrelacés. On réalise un noeud avec une corde que l'on emmêle et dont on soude les deux bouts ; on peut ensuite la déformer à loisir.

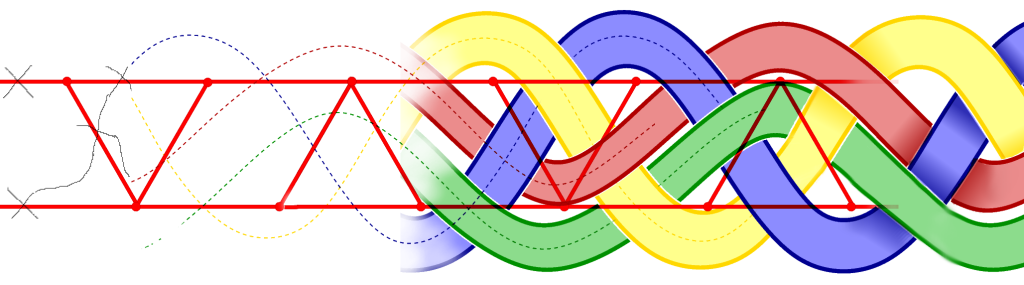
Pour représenter un entrelacs, on étale les cordes sur une surface plane en ne gardant que des croisements de deux cordes ou plus, et on dessine le tout en notant soigneusement à chaque croisement laquelle est au-dessus et laquelle est en dessous. Autrement dit, on réalise une projection régulière de celui-ci sur le plan.

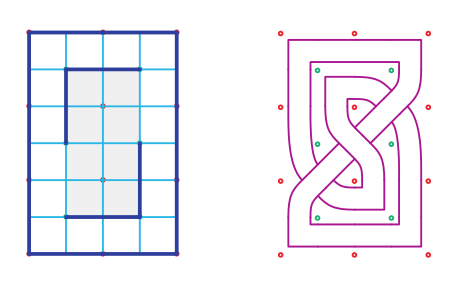
Pour visualiser la géométrie d’un entrelacs, on contaste que sa projection décompose le plan en composantes connexes : le graphe lui-même (de dimension 1), une zone infinie et des composantes homéomorphes à un disque (de dimension 2). En associant la couleur noire à la zone infinie et en alternant les couleurs noire et blanche à chaque passage d'une composante connexe (de dim. 2) à une autre, on obtient la figure gauche. Puis on construit un graphe planaire à arêtes signées qui représente les relations d'adjacences de la construction que l'on a précedemment obtenue (figure droite).

Le dessin d'un entrelacs repose donc sur un graphe dont chaque arête signée porte l'information du type d'intersection entre deux brins de l'entrelacs, où l'on indique l'information des dessus-dessous, et dont la position de chaque sommet influence la courbure de chaque brin.

On peut enrichir la structure, épaissir le trait, orienter chaque noeud, ne pas tous les fermer et maintenir leur extrémité fixe (on parle alors d'enchevêtrement), ou encore attacher une couleur à chaque noeud ou à chaque croisement.

A noter que cette méthode permet de construire des entrelacs de façon automatique mais de ce fait est assez limitée. Etant par nature déterministe, elle doit être considérée comme une première approximation mais peut se révéler néanmoins plaisante à regarder lorsque le nombre de croisements est important, c'est à dire lorsque l'impression générale domine l'exécution proprement dite.

Cahier des charges

Il existe de multiples façons de prendre en compte le graphe sous-jacent à la construction d'un entrelacs, citons entre autres références :

un algorithme par Andrew Glassner (PDF 1).
un tutoriel par Christian Mercat (PDF 2),
un article basé sur des motifs hyperboliques (avec une introduction générale) par Douglas Dunham (PDF 3),

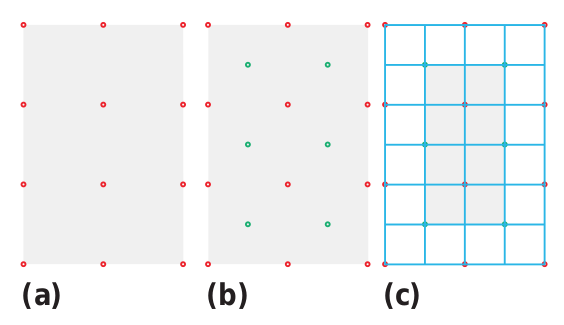
Dans le cadre de ce projet, on adoptera la méthode proposée par A. Glassner et on se limitera donc à un graphe (et son dual) dont les nœuds sont régulièrement répartis sur une grille cartésienne du plan euclidien.

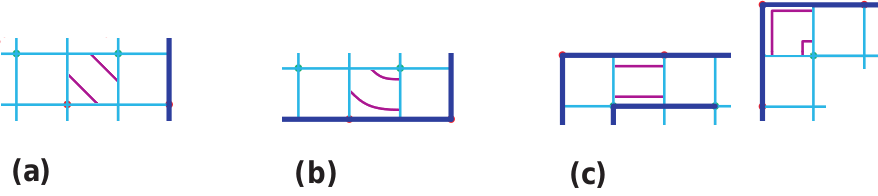
Glassner distingue trois grilles mais seule la première (a) doit être définie par l'utilisateur car les deux autres découlent de celle-ci. En pratique, l'algorithme repose sur la troisième grille (c).

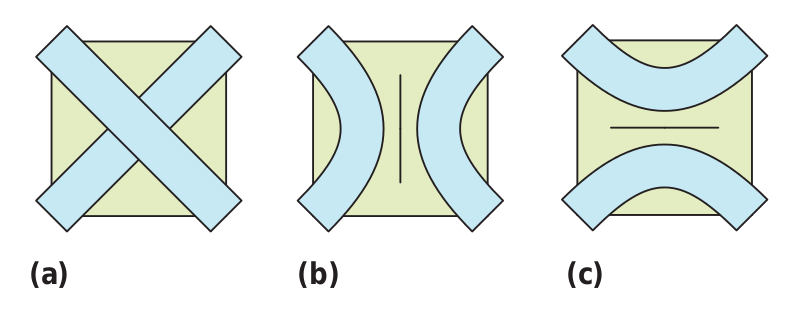
Des "murs" (pour reprendre la terminologie de l'article de C. Mercat) peuvent relier deux sommets voisins d'une même grille (la première ou la deuxième) soit horizontalement soit verticalement. Ces murs modifient la trajectoire des brins de l'entrelacs, qui du coup ne se croisent plus ((b) et (c) figure ci-dessous).

Selon l'absence ou la présence d'un mur et sa disposition, on peut obtenir quatres cas de figures : soit l'entrelacs se croise normalement, soit il suit une courbe ou une trajectoire rectiligne soit il forme un angle. L'épaisseur des traits (w) est pris en compte pour déterminer les positions de points extrémités de chaque portion d'entrelacs.

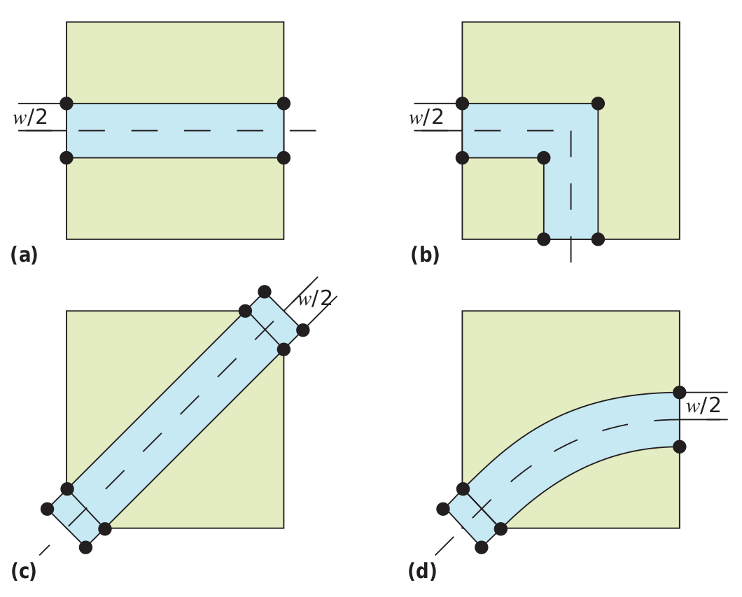
On peut observer l'utilisation des quatres configurations dans la figure suivante.

Glassner propose une méthode assez complète pour construire l'entrelacs mais il est possible d'adopter une méthode plus simple et, de ce fait, plus limité. Cette méthode repose sur l'observation de l'état de chacun des 4 voisins indirects (en diagonale) d'une arête du graphe ternaire :

si l'arête et l'arête voisine sont sans mur alors on construit une diagonale qui représente le lieu de croisement de l’entrelacs et pour lequel il faudra distinguer le dessus du dessous par la suite (a),
si l'arête est sans mur et que l'arête voisine comporte un mur alors on trace une portion de courbe (1/8ème de cercle par exemple), parallèle au mur et qui doit se terminer au niveau de l'arête non marquée de façon à pouvoir dessiner par la suite le "dessus-dessous" (b),
si l'arête et l'arête voisine comportent chacune un mur alors si les murs associés forment un angle droit, on construit un angle droit ; si par contre ils sont parallèles, on construit un segment horizontal ou vertical (c).

La dernière étape consiste à traiter les cas des "dessus-dessous". Pour ce faire, une stratégie simple, mais néanmoins justifiée par le type ce construction est d’alterner ceux-ci sur une droite horizontale. Ainsi, sur les colonnes d’indices impaires, on tracera un segment qui reliera la portion d’entrelacs inférieure-droite avec la portion d’entrelacs supérieure-gauche et sur les colonnes d’indices paires, on tracera un segment qui reliera la portion d’entrelacs inférieure-gauche avec la portion d’entrelacs supérieure-droite.

L'interface à réaliser doit permettre :

de choisir les dimensions du graphe primaire sur lequel on va travailler,
de modifier le graphe ternaire par ajout, modification (i.e changement d'orientation) et suppression de "murs",
de respecter l'ordre de construction (par exemple : inhibition du tracé de l'entrelacs tant que le graphe n'est pas défini),
de sauvegarder, de charger et d'initialiser un graphe,
d'associer des préférences à une session de travail (pas du maillage, épaisseur des traits, couleurs intérieures et extérieures de l'entrelacs, ...).

Quelques conseils

Travaillez modulairement, en particulier :

concernant le graphe, déterminez les formules qui caractérisent chaque noeud du graphe (i.e son rang) en fonction de la hauteur et de la largeur du graphe puis implantez des fonctions qui vous donneront certains renseignements utiles à la gestion du graphe, par exemple si un noeud appartient à une colonne (ou une ligne) paire ou impaire, s'il possède des voisins et lesquels, etc.,
de la même façon, pour la partie graphique, il est préférable d'écrire des procédures qui construisent des courbes et des segments de droites comportant suffisamment de paramètres pour répondre à tous les usages que vous en ferez,
maintenez une structure de données telle qu'une liste de tous les noeuds, des noeuds marqués (i.e avec mur) et non marqués (i.e sans mur) ainsi qu'un tableau associatif qui réunit pour chaque entrée (un noeud) le mur associé ainsi que son orientation.

Notation

La notation de ce projet prendra en compte le respect du cahier des charges, la qualité de la programmation (robustesse, lisibilité et modularité de votre code) ainsi que les aspects propres à une IHM que sont : cohérence, concision (limitation du nombre d’interventions de l’utilisateur), structuration des activités (décomposition d’une tâche complexe), flexibilité (application personnalisable), retour d’informations et gestion des erreurs, toutes choses qui garantissent une interface ergonomique et intuitive et qui n’apparaissent pas explicitement dans cette présentation.