Modélisation d'une scène

On se limitera à la construction d'une scène composée uniquement de cubes modélisés en perspective dimétrique (i.e dont la largeur de la face supérieure est deux fois plus longue que la hauteur).

Chacun de ces « cube » est affiché par ses trois faces visibles, celles-ci se distinguant les unes des autres par leur luminosité (avec un éclairage zénithal par exemple). Remarque : les couleurs nommées par X11 ne le sont pas de façon logique, par exemple pour le rouge red est plus clair que red3 alors que c'est l'inverse pour le vert i.e. green3 est plus clair que green.

Un cube est positionné soit interactivement sur une grille magnétique, soit par programme. Le choix d'un référentiel adapté est conseillé, ce qui implique des conversions de coordonnées entre le repère euclidien de la fenêtre graphique et le repère associé à la perspective dimétrique.

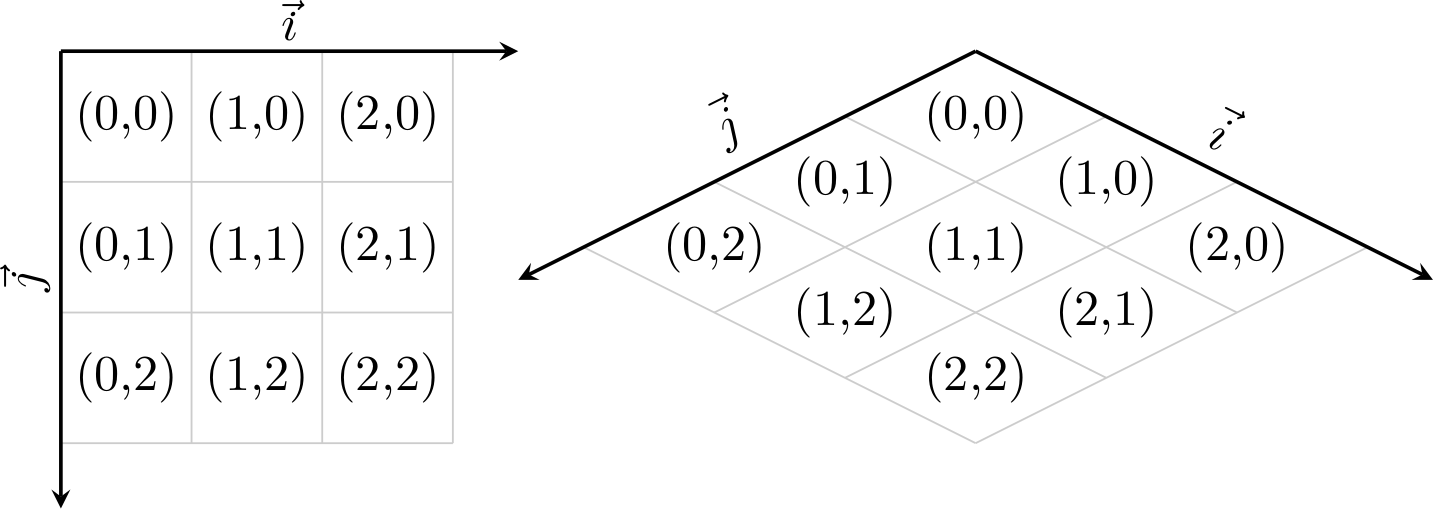
Les vecteurs directeurs du repère isométrique sont \(i = (2d, d)\) et \(j = (-2d, d)\) (avec le rapport 2:1, ces deux vecteurs sont bien orthogonaux) avec \(d\) la demi distance verticale entre deux points de la grille. Soit \(p = (a, b)\) un point dans ce repère et \(p' = (x, y)\) le même point dans le repère de la fenêtre graphique. On a la relation : \(p'(x, y) = (a i_1 + b j_1, a i_2 + b j_2)\). Ceci nous permet d'établir les équations de passage du repère cartésien au repère isométrique :

La mise en œuvre du magnétisme d'une grille facilitant le positionnement des cubes est rendu possible par la combinaison de tags judicieusement choisis pour les éléments de la grille et des méthodes find_overlapping ou find_closest du Canvas.

Affichage d'une scène

L'ordre d'affichage est primordial, car il permet de résoudre les problèmes de « vus et cachés » par la mise en oe uvre de « l'algorihme du peintre ». Celui-ci consiste à afficher les objets des plus éloignés aux plus proches par rapport à un observateur virtuel, ce qui résout simplement le problème de visibilité.

Dans le cas de la 3D isométrique, il suffit d'afficher les cubes en suivant l'ordre induit par le repère associé.

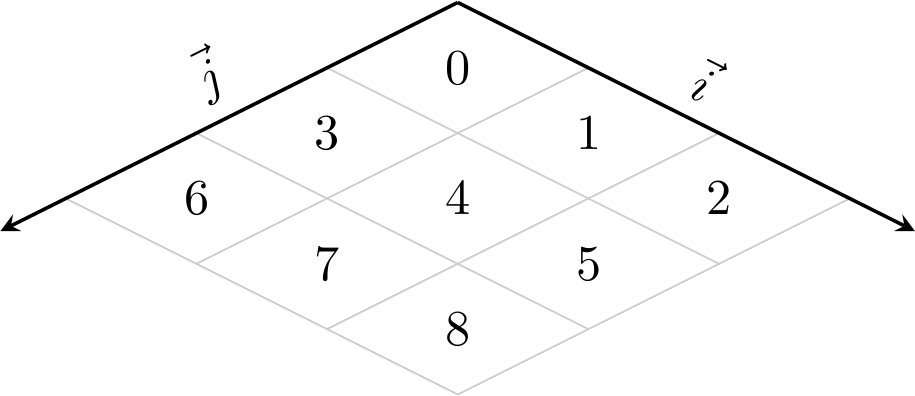
Modélisation en élévation

Il reste le problème du placement de cubes en « hauteur ». On remarque que ces cubes sont d'abscisse et d'ordonnée inférieures dans le repère de la 3D isométrique, par rapport aux cubes sur lesquels ils « reposent » (voir figure ci-dessous). Ceci pose évidemment un problème pour les bords de la grille de positionnement.

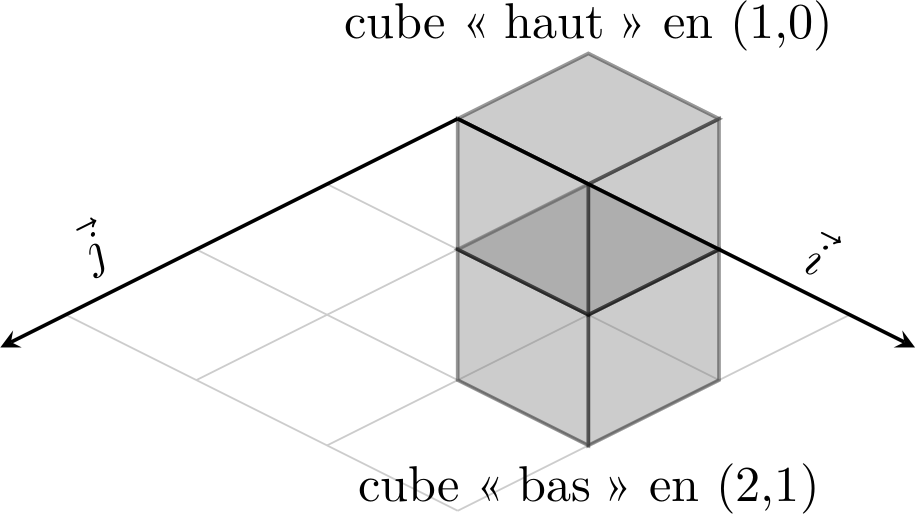
L'affichage en toute généralité devra se faire couche par couche, des cubes les plus « bas » aux cubes les plus « hauts ». Il faut donc prévoir un attribut de hauteur pour chaque instance de cube.

La prise en compte de ce paramètre lors du placement interactif des cubes est délicate. En effet, en fonction des hauteurs relatives des cubes qui se recouvrent, ceux-ci doivent respecter un ordre d'affichage (on utilisera avec profit les méthodes tag_lower et tag_raise de Canvas) :

• si un cube est plus bas qu'un autre, il doit s'afficher avant ce dernier,
• si un cube est plus haut qu'un autre, il doit s'afficher après ce dernier,
• si les deux cubes sont à la même hauteur, l'ordre d'affichage est conditionné par la position relative de leur référentiel dans le repère isométrique (et donc de la projection de leurs coordonnées depuis le repère cartésien de la fenêtre).

Visualisation

Il possible d'obtenir un rendu bien plus attrayant en attachant à chaque cube une texture tirée d'une image (tileset) telle que celle représentée ci-dessous.

Cette possibilité est offerte par le module PIL, plus précisément les classes Image et ImageTk. Le chargement d'une image et l'extraction d'une région de cette image (tile) se font via Image, et le lien avec tkinter se fait par ImageTk, par exemple :

im = Image.open(filename)
im = im.transform((tile_width, tile_height), Image.EXTENT, (x0, y0, x1, y1))  # region de l'image
im.thumbnail((final_width, final_height))  # mise a l'echelle
imp =  ImageTk.PhotoImage(im)
id = canv.create_image(x, y, image=imp, anchor='center')

Cahier des charges

Dans ce projet, on s'attachera à la conception d'un programme basé sur le paradigme objet et d'une interface ergonomique.

Une phase de conception préalable, qui repose sur des diagrammes UML de structure (en particulier classes et objets) et de comportement (en particulier « cas d'utilisation ») ou sur une conception dirigée par les buts (avec archétypes, scénarios et décomposition associée), est fortement conseillée.

Les fonctionnalités demandées, volontairement approximatives, sont par ordre d'importance décroissante :

• de définir interactivement ou par commandes une scène en 3D isométrique,
• de choisir couleurs et « hauteur » des cubes,
• d'offrir une aide en ligne si possible contextuelle,
• de modifier ou de supprimer des parties de la scène,
• de sauvegarder et de charger des scènes,
• de paramétrer les constituants de l'application,
• d'associer des pixmaps aux cubes.

L'implantation de l'application doit être modulaire (grossièrement, une classe par module), en Python objet, et utiliser la bibliothèque tkinter pour l'interface graphique.

Une attention particulière doit être portée à l'utilisation des paradigmes objets. La définition d'au moins deux classes (Cube et un conteneur de d'instances de Cube) et l'utilisation des propriétés afin d'offrir un moyen transparent de définition d'accesseurs et de mutateurs, sont obligatoires.

Exemple de mise en œuvre des propriétés pour la protection des attributs d'une classe :

class P:

    def __init__(self, px):
        self.__xx = px

    @property
    def x(self):
        """ double mangling """
        return self.__xx

    @x.setter
    def x(self, px):
        """ 0 <= self.x <= 1000 """
        if px < 0:
            self.__xx = 0
        elif px > 1000:
            self.__xx = 1000
        else:
            self.__xx = px

p1 = P(10)
print('p1.x', p1.x)
p1.x = 2000

Exemple de mise en œuvre d'une classe conteneur utilisant un dictionnaire comme attribut :

class MonDico(dict):
    def __setitem__(self, key, value):
        # pretexte : non modifiable
        if self.get(key) is not None:
            raise KeyError('La clé existe déjà')
        else:
            super().__setitem__(key, value)

class A(object):
    def __init__(self, pdd):
        self.__dd = MonDico(pdd)

    @property
    def dd(self):
        return self.__dd


a1 = A({'a':1, 'b':2})
a1.dd['c'] = 3  # /!\ accesseur de A puis mutateur de MonDico
print(a1.dd)
a1.dd['a'] = 3

Notation

La notation de ce projet prendra en compte le respect du cahier des charges, la qualité de la programmation (robustesse, lisibilité et modularité du code, présence de tests unitaires) ainsi que les aspects propres à une IHM que sont : cohérence, concision (limitation du nombre d’interventions de l’utilisateur), structuration des activités (décomposition d’une tâche complexe), flexibilité (application personnalisable), retour d’informations et gestion des erreurs, toutes choses qui garantissent une interface ergonomique et intuitive et qui n’apparaissent pas explicitement dans cette présentation.