Projet OpenGL - Système solaire
Objectifs
A partir des éléments de MESA vus au cours des précédents TP, réaliser la modélisation du système solaire. L’utilisateur doit avoir la possibilité de se déplacer autour du système (rotation, translation, zoom) ou de suivre la trajectoire d’une fusée, ceci de facon interactive par l’intermédiaire de la souris ou de touches du clavier. Les mouvements des astres ainsi que de la fusée équipée d’un unique réacteur (à l’arrière) devront être réaliste, c’est à dire suivre les lois de la mécanique classique.
Modélisation des planètes
Le système solaire est constitué de neuf planètes. Dans l’ordre en partant du Soleil on trouve : Mercure, Vénus, la Terre, Mars, Jupiter, Saturne, Uranus, Neptune et Pluton. Elles gravitent toutes approximativement dans un même plan contenant le centre du Soleil : l’écliptique. L’inclinaison du plan de l’orbite sur l’écliptique varie de 0° à 3° 23’, excepté pour Mercure (7° 00’) et Pluton (17° 09’). Les trajectoires des planètes sont des ellipses. A l’exception de Mercure et Pluton, ces trajectoires sont quasiment assimilables à des cercles.
Vu du Nord, toutes les planètes tournent autour du Soleil dans le sens anti-horaire. De plus, à l’exception de Vénus, les planètes tournent sur elles-mêmes dans le sens de leur révolution autour du Soleil.
Leur modélisation correspond à de simples sphères, sur lesquelles sont plaquées les textures ci-dessous :



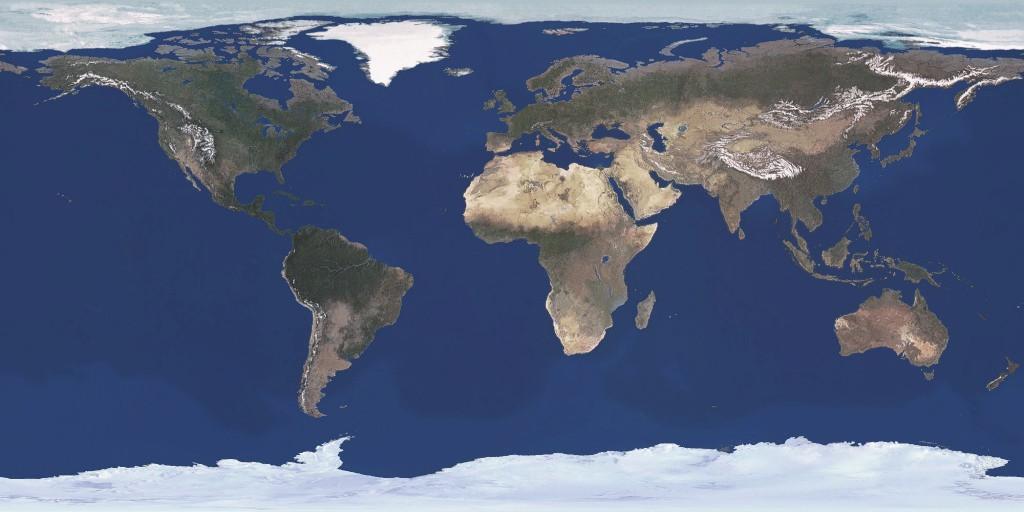

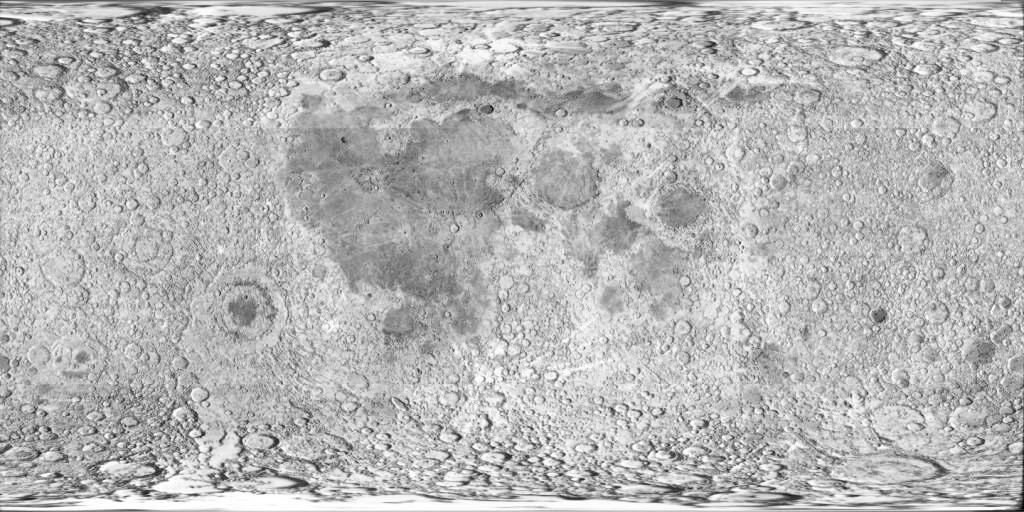






Concernant leurs caractéristiques physiques, celles-ci sont résumées ici.
Interaction
Elle consiste en une animation de la caméra et de la fusée en tenant compte pour cette dernière des forces mises en jeu, c’est-à-dire celles du soleil et des planètes ainsi que celle du réacteur. La poussée de ce dernier pourra être augmentée ou diminuée par l’utilisateur. La caméra pourra être libre ou focalisée sur la fusée, à une distance constante tant que l’utilisateur ne change pas cette distance (elle pourra continuer à subir des rotations autour du point que constitue la fusée). Enfin, l’application doit offrir la possibilité de changer le pas de discrétisation (i.e les intervalles de temps, dt dans les rappels de mécanique ci-dessous).
Rappels de mécanique
Force de gravitation
Soient deux solides P1 et P2, respectivement de masse m1 et m2 et de position M1 et M2, la force qu’exerce P2 sur P1, notée f2->1 s’exprime par :
f2->1 = c m1 m2(M1M2 / ||M1M2||3) avec c : constante gravitationnelle
Remarque : le dénominateur est bien élevé au cube, car la force de gravitation est en 1/r2 (et on normalise le vecteur)
Accélération, vitesse et position
Soit un solide en mouvement de masse m1, son accélération peut se calculer par :
a1 = somme(forces) / m1
Dans le cas qui nous occupe (fusée), il faut ajouter à a1, l’accélération dûe au réacteur.
Ceci nous permet d’en déduire sa vitesse et donc sa position :
v1(t + dt) - v1(t) = a1(t) dt
M1(t + dt) - M1(t) = v1(t) dt
Vitesse angulaire
La rotation d’une sphère sur elle-même durant son déplacement, ou vitesse angulaire, s’exprime par la relation :
Vr = -Vt/R
avec Vr : vitesse de rotation, Vt : vitesse de translation, R : rayon de la boule.
Personnalisation du projet
Trois possibilités s’offrent ą vous :
- un projet pédagogique : l’utilisateur doit avoir la possibilité d’interroger, par “picking”, l’ensemble des objets de la simulation et d’en déduire des informations liées ą la simulation,
- une simulation : on portera une attention toute particulière ą l’exactitude des paramètres de la simulation (inclinaison, vitesse, etc.), du rendu (visualiser des nuages au dessus de la Terre, des anneaux de Saturne, etc.), de la simulation du vol (jet de gaz à la sortie du réacteur de la fusée, etc.).
- un jeu : l’utilisateur doit avoir la possibilité de se mettre en vue subjective (cabine de la fusée), ou en mode “caméra intelligente)