Les surfaces spiroïdales

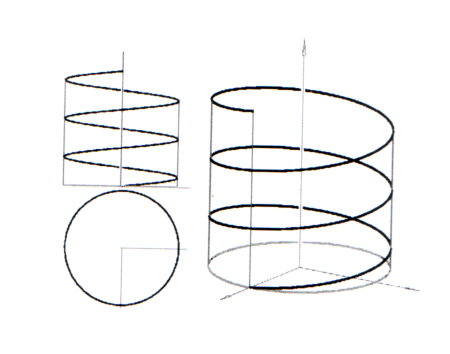
Déplacement hélicoïdal : soit un axe a dans l'espace euclidien 3D, ce déplacement est la combinaison d'une rotation autour de a à vitesse angulaire constante et d'une translation le long de a à vitesse également constante. La relation qui lie l'angle a de rotation et la longueur l de la translation peut s'écrire :

$ p Î R*, l = p.a

On constate que la courbe résultante s'inscrit sur la surface d'un cylindre de révolution d'axe a.

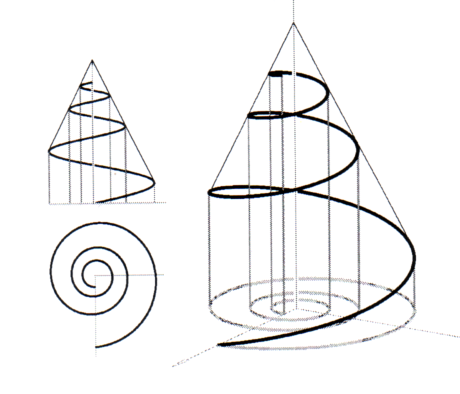
Déplacement spiralé : soit le même axe a et un point fixe O sur a (point asymptotique), une spirale est une famille continue de rotations élastiques, chacune d'entre elles étant le produit (commutatif) d'une rotation autour de a et d'une homothétie de centre O, ce que l'on peut écrire :

$ p Î R*, s = e^pa

s est appelé facteur d'"élasticité".

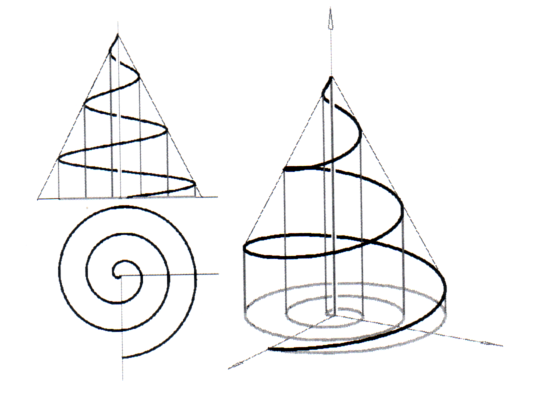
Une trajectoire spiralée est contenue dans un cône de révolution d'axe a et de sommet O. Sa projection normale à un plan P contenant O, perpendiculaire à a, est une spirale logarithmique.

Surface spiralée : elle est obtenue en appliquant un déplacement spiralée (a, O, p) à une courbe k (qui ne doit pas être elle-même une spirale).

Approche analytique : nous décrivons ci-dessous les courbes et les surfaces spiroïdales dans un système de coordonnées cartésien.

Courbe passant par P(x₀, y₀, z₀) :

x(a) = e^pa(x₀ cos a - y₀ sin a)

y(a) = e^pa(x₀ sin a + y₀ cos a)

z(a) = z₀ e^pa

Surface paramétrée par la courbe (x(u), y(u), z(u)) :

x(u,a) = e^pa(x(u) cos a - y(u) sin a)

y(u,a) = e^pa(x(u) sin a + y(u) cos a)

z(u,a) = z(u) e^pa

Exemple d'application :

Une ellipse comme courbe génératrice,soient r et s les demi-longueurs de l'axe primaire et secondaire, on a :

x(u) = s + s cos u

y(u) = 0

z(u) = r sin u

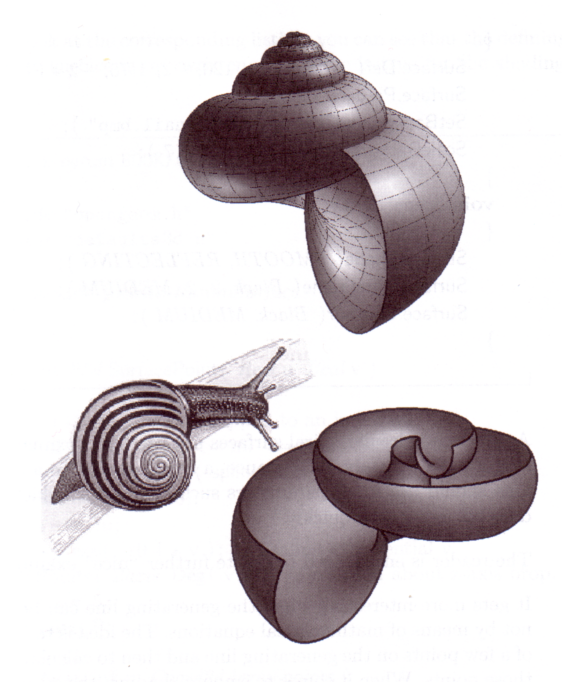
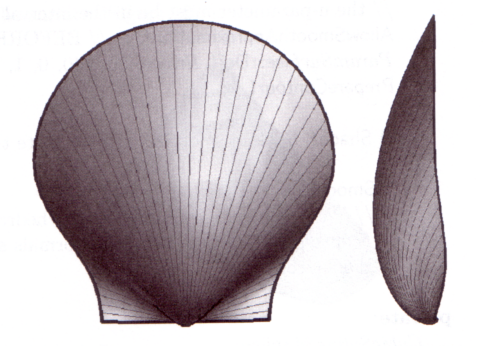
(avec u Î [0, 2p], r = 35, s = 25 et p = 0,4 par exemple image de gauche)

On pourra aussi mettre à profit ses connaissances sur les courbes splines en les utilisant comme courbe génératrice (les deux images de droite).

Les surfaces hélispiroïdales

Surfaces à la fois hélicoïdales et spiroïdales, elles s'expriment comme la combinaison d'une rotation d'angle a autour d'un axe a et d'une dilatation proportionnelle (non exponentielle) à p (facteur de proportion) pa par rapport à un point fixe O Î a.

Soient O(0, 0, s) et p, la trajectoire d'un point (r₀, j₀, z₀) en coordonnées cylindriques est décrite par le paramètre temporel t :

r = p.t.r₀

j = j₀ - 1/p + t

z = s + p.t (z₀ - s)

L'équation paramétrique d'une rotation autour d'un axe a, d'un angle 1/p - j₀ s'écrit :

x(t) = p.t.r₀ cos t

y(t) = p.t.r₀ sin t

z(t) = s + p.t (z₀ - s)