Objectifs

A partir des éléments vus en cours et en TD, réaliser une application qui recherche un plus court chemin à partir du partitionnement d’un plan cadastral.

Principes

Une stratégie de recherche d’un (plus court) chemin dans un plan, qui comporte des obstacles sous forme polygonale, est de subdiviser le domaine puis de construire le chemin.

L’espace de configuration \(\mathcal{C}\) représente l’espace paramétrique propre au mobile. Les points de \(\mathcal{C}\) qui correspondent à une intersection entre le robot et un obstacle doivent être exclus. Soit \(S\) l’ensemble des obstacles, on défini l’espace de configuration interdit \(\mathcal{C}_p(\mathcal{R}, S)\) et l’espace de configuration libre \(\mathcal{C}_f(\mathcal{R}, S)\).

Plutôt que de représenter le chemin explicitement, on construit une représentation de l’espace de configuration libre \(\mathcal{C}_f\), ce qui est efficace si l’espace de travail \(\mathcal{C}\) ne change pas et si plusieurs chemins doivent être planifiés.

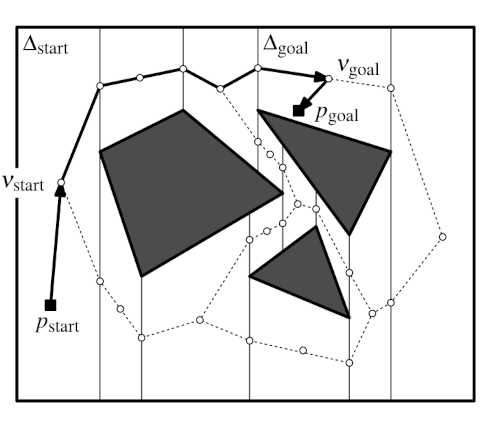
On restreint l’espace des solutions à une boîte englobante de l’ensemble des obstacles (ce qui revient à créer un obstacle infini à l’extérieur). On peut construire une représentation de cet espace par une carte trapézoïdale (un trapèze est un quadrilatère possédant deux côtés opposés parallèles, ces deux côtés parallèles sont appelés bases). Cette représentation se fait par balayage du domaine par une “scanline” passant par chaque sommet des polygones.

Chaque ligne de balayage débute à un sommet et se prolonge, par exemple verticalement vers le haut et vers le bas, jusqu’à rencontrer une arête ou la limite du domaine. L’élimination des portions de lignes intérieures aux polygones aboutit à la carte trapézoïdale.

A partir de la représentation de l’espace de configuration libre \(\mathcal{C}_f\) par cette carte trapézoïdale, on peut établir un graphe sous-jacent dont les noeuds sont successivement le milieu de la première base, le barycentre, et le milieu de la seconde base de chaque trapèze. Ce graphe est le support de recherche d’un chemin.

Conception et implantation

Une conception modulaire est demandée.

L’unique fichier de données fourni correspond au plan cadastral de la ville de la Garde : cadastre-83062-batiments.json.gz. On prendra soin de travailler dans l’espace discret.

Ce projet se prête à une implantation progressive.

1. chargement et affichage du plan cadastral : ce dernier étant au format json, on utilisera le module json (et sa fonction load()),
2. sélection au choix de la portion du plan qui inclut uniquement des bâtiments de l’université de Toulon (aux environs des bâtiments 5900 jusqu’à 6200, non compris les bâtiments 6194 et 6195) et affichage : la sélection se fait de façon statique dans le programme (et non de façon interactive),
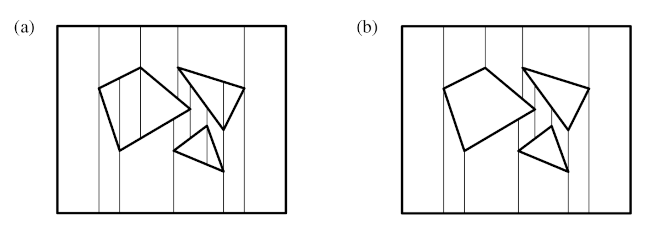
3. définition de l’enveloppe convexe de chaque bâtiment (par souci de simplification) : le rectangle englobant est une enveloppe convexe grossière, en identifiant chaque sommet d’un polygone comme formant un angle ouvert ou fermé, il est possible de construire une enveloppe convexe plus précise,
4. construction de la carte trapézoïdale en subdivisant le domaine par lignes de balayage (scanline) : on calculera les points d’intersection avec les polygones de façon à préparer l’étape suivante,
5. représentation de l’espace de configuration libre par élimination des portions de segments internes aux polygones (convexes) : on prendra soin d’adopter une structure de données adaptée,
6. construction du parcours sous la forme d’un graphe planaire : même remarque que précédemment,
7. recherche du (plus court) chemin et affichage : on peut simplement afficher l’un des chemins ou rechercher le plus court par l’algorithme de Dijkstra (ou mieux, l’algorithme A*).

Évaluation

Ce projet est un prototype pour lequel un certain nombre de fonctionnalités sont demandées :

1. définition de l’enveloppe convexe de chaque bâtiment,
2. décomposition du domaine par une carte trapézoïdale,
3. représentation de l’espace de configuration libre,
4. recherche et affichage du (plus court) chemin entre deux points du domaine,

L’implantation devra se faire en Python, l’affichage utilisera le module tkinter (l’utilisation de matplotlib est autorisée, voire conseillée pendant la phase de développement, mais s’accompagnera d’un malus).

Chaque objectif du projet ainsi que la qualité de l’implantation sera évalué sur 4 points. Une archive comportant tous les fichiers nécessaires à l’exécution du projet devra être remise à l’enseignant pour évaluation.