Objectifs

A partir des éléments vus en cours et en TD, réaliser une application illustrant les notions fondamentales de recherche d'un plus court chemin. L'implantation devra se faire en Python, à l'aide des bibliothèques standards et de la bibliothèque graphique pyopengl.

Conception

Modèles de données

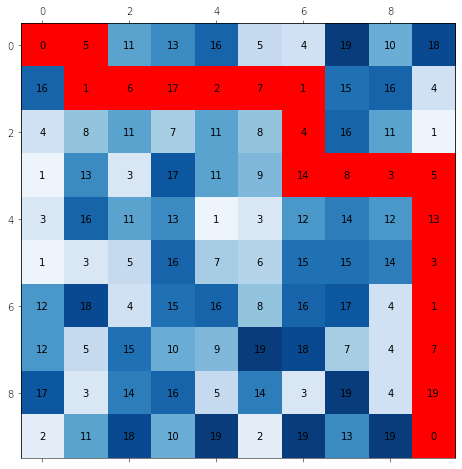
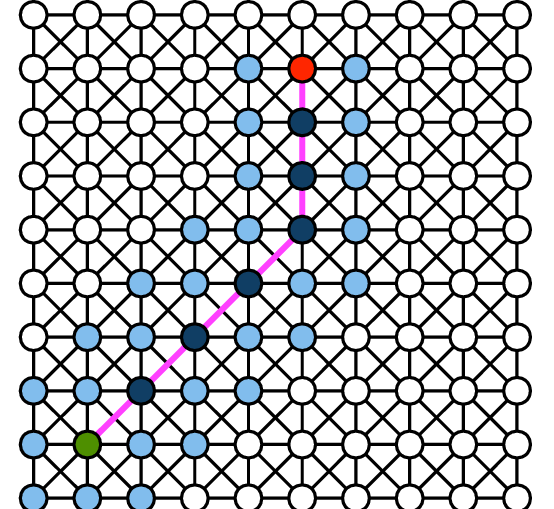
Les algorithmes de recherche du plus court chemin travaillent le plus souvent sur un graphe orienté valué. Pour les adapter à la recherche d'un chemin sur un modèle de terrain, on peut travailler sur une représentation intermédiaire.

Cette représentation peut prendre la forme d'une matrice M de valeurs entières positives correspondants au coût de passage par un élément de cette matrice. La notion de voisinage peut être directe ou indirecte, dans ce second cas il suffit d'appliquer un coût supplémentaire de l'ordre de \(\sqrt{2}\). Afin d'éviter de traiter des cas particuliers, il est recommandé d'ajouter à la matrice initiale une "bordure" de valeurs particulières permettant de normaliser les traitements à effectuer y compris aux bords de la matrice.

Des structures intermédiaires sont à prévoir pour d'une part pouvoir actualiser le coût du chemin du point de départ à un élément de la matrice (futur terrain) et d'autre part retrouver le chemin le plus court une fois le but atteint. Pour le premier point, une matrice de même dimension que la matrice des coûts est nécessaire et pour le deuxième point un simple tableau de correspondance permettra de mémoriser les relations entre voisins successifs du chemin trouvé. Il faut ajouter à cela un modèle de données optimisant la recherche du prochain point du chemin le moins coûteux sous la forme d'un tas (heap).

Après application des algorithmes de recherche d'un plus court chemin entre un point de départ et d'arrivée choisis préalablement (y compris par une simple saisie dans un terminal des coordonnées des deux composantes de la matrice), la mémorisation des résultats obtenus permet de passer de la résolution d'un problème théorique à la représentation 3D d'un modèle de terrain et du cheminement d'un mobile le long du chemin trouvé.

Représentation 3D de la matrice des coûts

Le terrain s'appuie sur les valeurs de la matrice pour être représenté en élévation 3D, ce qui signifie que les coûts de passage correspondent à des altitudes (ou plus généralement à des types de terrain). Dans le cadre du projet, on se contentera de représenter chaque valeur M[i][j] de la matrice par un carré à une hauteur correspondant à cette valeur. Cependant, la transformation d'une matrice de valeurs en élévation 3D n'est pas directe, elle nécessite une adaptation qui consiste à insérer des espaces intermédiaires entre chaque carré, de façon à créer des jonctions moins abruptes que de simples plans verticaux. Cela peut se faire par une relation simple entre les indices i, j de la matrice et les coordonnées \((2i, 2j), (2i+1, 2j), (2i+1, 2j+1)\) et \((2i, 2j+1)\) dans le plan XY des sommets des carrés correspondants, la troisième composante de chaque sommet se déduisant de la valeur M[i][j] de la matrice.

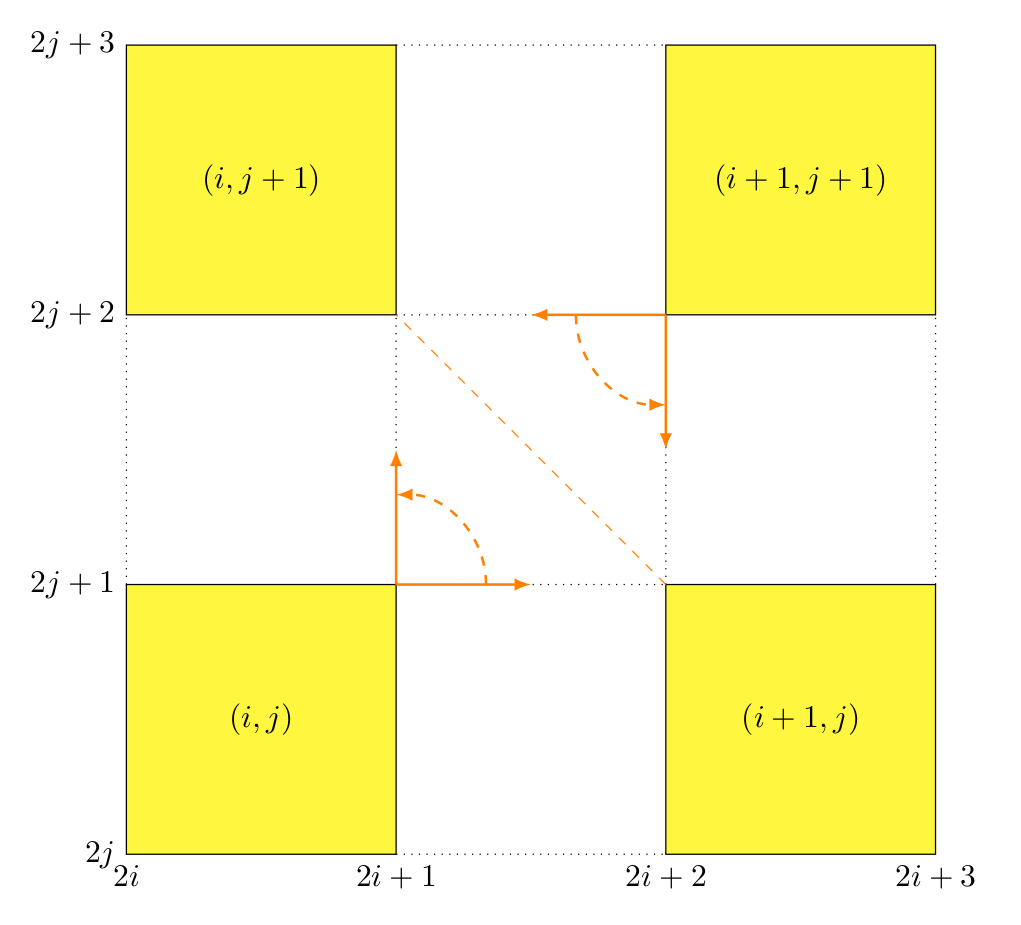
La création des jonctions est simple puiqu'il suffit de récupérer les valeurs (x, y, z) des sommets idoines pour modéliser chaque facette manquante du maillage, celle-ci étant de forme rectangulaire ou triangulaire (uniquement triangulaire si l'on souhaite unifier la représentation). Mais il faut aussi déterminer les normales aux facettes ainsi créées afin de garantir un affichage cohérent.

Concernant les normales aux facettes carrées issues directement de la matrice M, la détermination de leurs composantes est immédiate : il s'agit du vecteur unitaire perpendiculaire à ces facettes (a priori le vecteur (0, 1, 0)). Pour les facettes intermédiaires, la détermination des composantes de la normale se fera grâce au produit vectoriel de deux vecteurs orthogonaux dans le plan d'une facette qu'il est assez simple à déterminer. L'exemple le plus général est donné dans la figure ci-dessus concernant la facette commune aux quatre carrés originaux (les vecteurs de couleur orange). Il faut prendre garde à l'ordre des opérandes, celui-ci doit respecter le sens trigonométrique afin de déterminer la normale adéquate (et non son opposée), sous peine de ne pas obtenir le bon rendu.

Modélisation et mouvement du mobile

Le mobile se présente sous la forme d'un ver (worm) modélisé par une succession de sphères de diamètre décroissant et qui s'interpénètrent.

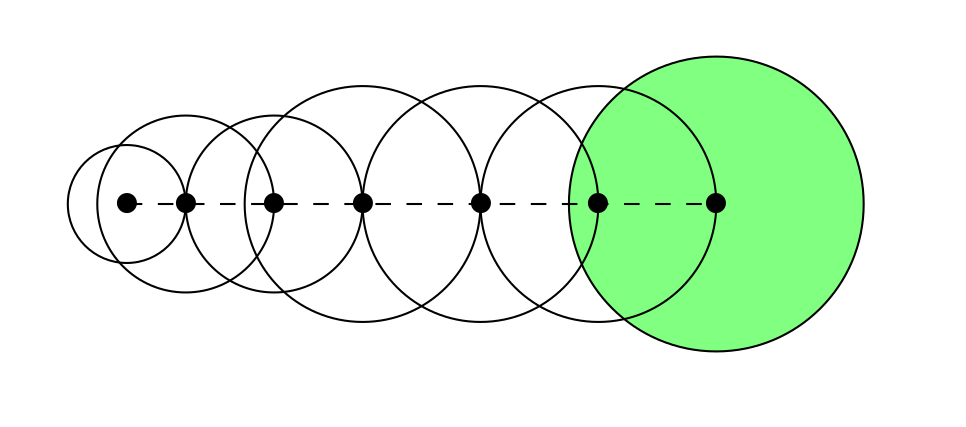
Le mouvement dans le plan XY du mobile est déterminé par la première sphère et le calcul des positions des sphères suivantes se fait en tenant compte des liaisons rigides entre chaque sphère.

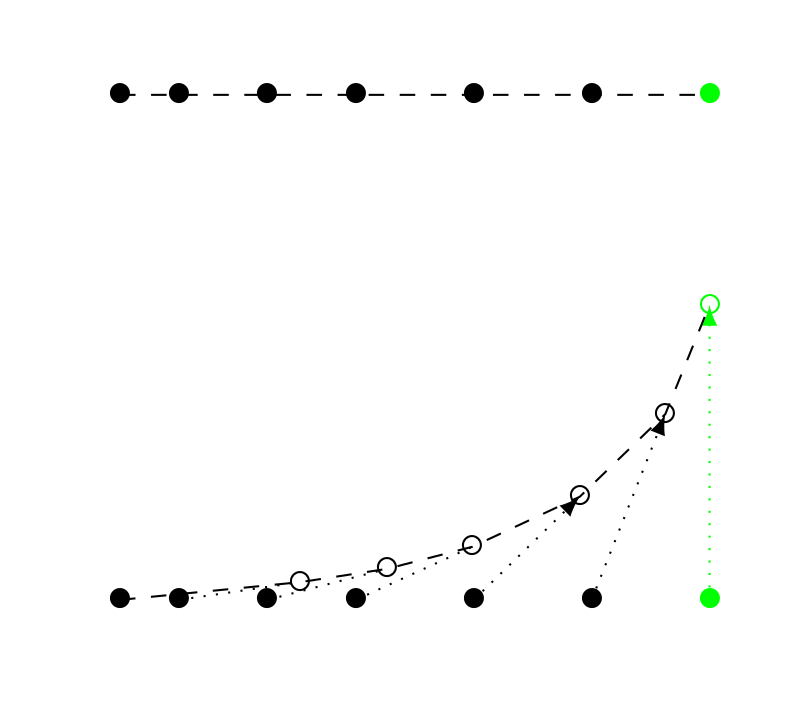
Le mouvement complet de la première sphère dans l'espace se fait d'une part dans le plan XY en interpolant les positions par l'intermédiaire de courbes de Bézier cubiques, dont les points de contrôle sont les positions successives du chemin trouvé (en garantissant uniquement la continuité \(C^0\)), et d'autre part en Z en interpolant les positions d'une sphère à la suivante à partir de la donnée des pentes sur lesquelles elles évoluent.

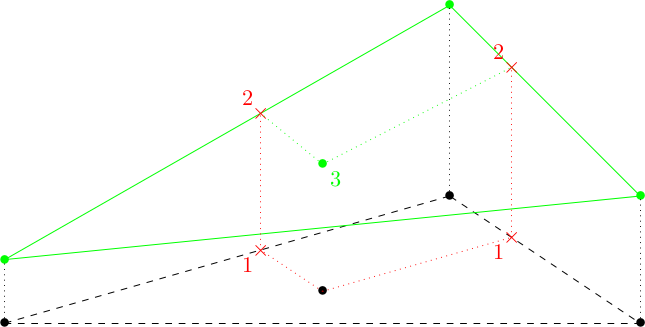
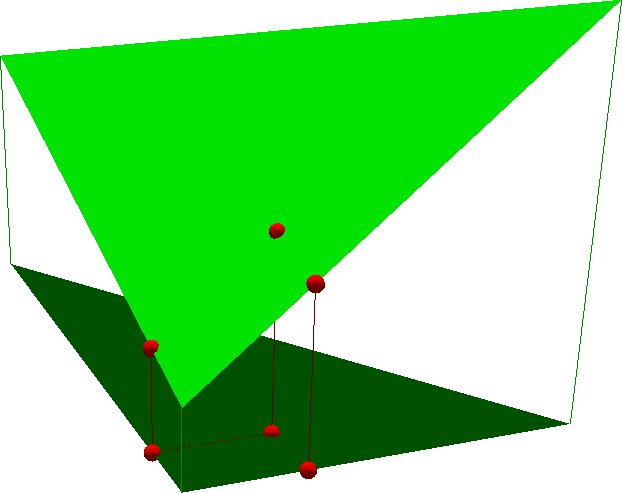
Le calcul des positions est bien entendu trivial concernant les portions de terrain horizontales. Celui associé aux carrés inclinés est très simple puisqu'il suffit de prendre en compte leur pente associée. Il en va de même lorsque le mobile suit l'arête de séparation de deux triangles. Le dernier cas, un trajet passant par l'intérieur d'un triangle, nécessite de calculer les positions 3D par projection des positions 2D. L'une des solutions peut se faire en trois étapes :

1. projection du point dans le plan XY sur les deux arêtes de l'angle droit du triangle 2D (par produit scalaire),
2. calcul de l'intersection de la droite verticale passant par ce point projeté et des deux arêtes du triangle 3D (en utilisant l'équation de la droite paramétrique associée à chaque arête),
3. calcul de la position du point dans le triangle 3D.

Implantation

Une implantation modulaire (et objet) se prête naturellement à ce type de problème. Il n'est pas demandé une application unique intégrant toutes les fonctionnalités et il est même conseillé de développer deux applications distinctes (l'une pour la recherche des chemins, l'autre pour la visualisation 3D de la solution).

La représentation de la matrice peut se faire par l'intermédiaire du module numpy pour des raisons d'efficacité (voir pour cela array). Numpy fournit par ailleurs le symbole d'une valeur infiniment grande (inf), utile pour implanter les algorithmes mis en oeuvre.

La nécessaire gestion d'un tas peut être confié au module heapq (voir pour cela heappush et heappop).

Il est nécessaire (et obligatoire) d'implanter des fonctions utiles au projet (recherche des voisins d'un élément d'une matrice, calcul de la normale à un polygone, etc.).

Il est recommandé mais non obligatoire d'implanter une version graphique 2D de la représentation de la matrice et du chemin trouvé. De même, il est recommandé d'implanter des outils d'aide à la modélisation 3D (gestion d'une caméra, affichage des normales, affichage de points caractéristiques, etc.).

Evaluation

Ce projet est un prototype (les performances purement graphiques ne seront pas pris en compte) qui doit intégrer un certain nombre de fonctionnalités :

1. codage, sauvegarde et chargement d'une matrice à valeurs entières,
2. choix d'un point de départ et d'un point d'arrivée, application des algorithmes de Dijkstra et A* et mémorisation des résultats,
3. affichage de la matrice sous la forme d'un terrain en élévation,
4. déplacement d'un mobile le long de l'un des chemins trouvés au choix (de préférence sous la forme d'un ver, sinon modélisé par une simple sphère) dont les mouvements seront calculés par l'intermédiaire d'une succession de courbes de Bézier cubique,
5. ajout d'un obstacle infranchissable dans la génération du terrain et pris en compte par les algorithmes de recherche de chemin,
6. gestion d'une caméra offrant une vue générale et des mouvements en translation, rotation et zoom (sans utiliser glutSpaceball*),
7. représentation des obstacles infranchissables sous la forme de zones aquatiques (ou équivalents),
8. suivi du mouvement du mobile par la caméra durant son parcours du chemin,
9. application de textures (terrain et mobile).

Les cinq premiers objectifs du projet ainsi que la qualité de la programmation (dont la présence de commentaires pertinents) seront évalués sur la base de 16 points, les autres aspects seront évaluées sur la base de 4 points. Une archive comportant tous les fichiers nécessaires à l'exécution du projet devra être remise à l'enseignant pour évaluation.

Les deux projets les plus aboutis auront par la suite une vitrine ci-dessous.