Projet OpenGL - Marble Madness
Objectifs
A partir des éléments de MESA vus au cours des précédents TP, réaliser la modélisation d’un jeu basé sur le déplacement d’une bille en acier sur un parcours en 3D, connu dans les jeux vidéo sous le nom de “Marble Madness”. La modélisation du terrain pourra être fixée une fois pour toute ou reposer sur un éditeur. L’environnement devra correspondre au modèle réel : déplacement, frottement, choc, attraction magnétique, …, par contre on supposera que la bille reste “scotchée” au sol. Un joueur a gagné la partie lorsqu’il est parvenu à atteindre le point d’arrivée. Pour se faire, il a la possibilité d’influer sur la trajectoire de la bille, en appliquant des forces perpendiculaires à la direction du mobile. L’utilisateur aura aussi la possibilité de mettre le jeu en pause et de se déplacer autour du plateau de jeu (rotation, translation, zoom), ceci de facon interactive par l’intermédiaire de la souris ou de touches du clavier. Les mouvements de la bille devront être “réalistes”, c’est à dire dans notre cas suivre les lois de la mécanique classique.
Principes du “Marble Madness”
Arrivé dans les salles d’arcades en 1984, sur borne Atari System 1, Marble Madness est un jeu d’adresse dans lequel vous pilotez une petite boule dans un décor 3D afin de coller au mieux au parcours imposé et atteindre la ligne d’arrivée. En plus de la gestion de l’inertie du mouvement de la boule, vous devez gérer les différents obstacles qui se dressent sur votre chemin (pièges, flaques, etc…) tout en ne dépassant pas le temps limite.
Dans le cadre de ce projet, la bille subit un nombre limité de forces : de gravité, de frottement, d’attraction et de l’utilisateur.
Pour une autre étude, voir “Marble Madness”.
Modélisation du “Marble Madness”
Quelques idées de modélisation …
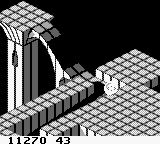
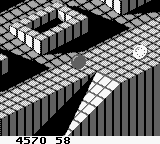
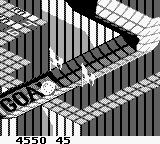
Interaction
Elle consiste simplement à pouvoir appliquer à tout instant une force perpendiculaire à la direction de la bille (d’un côté ou de l’autre) et parallèle au plan dans lequel elle est en train d’évoluer (voir rappels de mécanique ci-dessous). De plus, l’utilisateur doit pouvoir se déplacer autour du jeu. Il doit aussi avoir la possibilité d’activer/désactiver certaines options de rendu (texture, lumière, …) afin de pouvoir adapter l’application aux impératifs matériels.
Etude mécanique
Le terrain S sur lequel évoluera la bille doit être modélisé par un maillage triangulaire ou rectangulaire, avec un pas de résolution que l’on vous conseille fixe et petit (les grandes surfaces ne sont pas adaptées à l’approche choisie).
La bille est ramenée à une masse ponctuelle (de masse m = 1, pour éviter de compliquer les calculs inutilement) se déplaçant dans le plan de chaque élément de surface. On discrétise le temps, en décomposant le déplacement par petits intervalles de temps, afin de transformer l’équation différentielle régissant le mouvement en une équation algébrique explicite.
Notre masse ponctuelle est caractérisée par P(x, z, Vx, Vz). En effet, la connaissance de x, z et S (resp. Vx, Vz et S) permet de calculer y (resp. Vy).
| x = x + µ Vx | Vx = Vx + µ Ax | Ax = 1/m Fx | |||
| position | vitesse | accélération | |||
| z = z + µ Vz | Vz = Vz + µ Az | Az = 1/m Fz |
Les forces mises en jeu
F = Fg + Ff + Fa + Fm (Fg : gravité, Ff : frottement, Fa : attraction, Fm : “moteur”)
- Fg = (0, -m*g, 0) = (0, -g, 0) avec *m = 1
- Ff = -k (Vx t1 + Vz t2), avec k coef. de frottement (fluide), Vx et Vz les composantes en x et z du vecteur vitesse et t1, t2 les vecteurs tangents à l’élément de surface considéré (voir ci-dessous).
- Fa = K d/||d||3 avec K coef. d’attraction et le vecteur d = (x, y, z) - (a, b, c) (distance entre la bille et un point de l’attracteur).
- Fm = P(e) (N^V/||V||) avec P(e) une fonction dépendant des actions de l’utilisateur et rendant un scalaire, N le vecteur normal à l’élément de surface considéré et V le vecteur vitesse (à normaliser).
Les vecteurs tangents en un point de la surface
Soient t1 et t2 les vecteurs tangents au plan contenant la facette considérée :
t1 = (1, dy/dx, 0)
t2 = (0, dy/dz, 1)
t1 peut se calculer facilement en considérant l’intersection du plan vertical passant par x et du plan contenant la facette
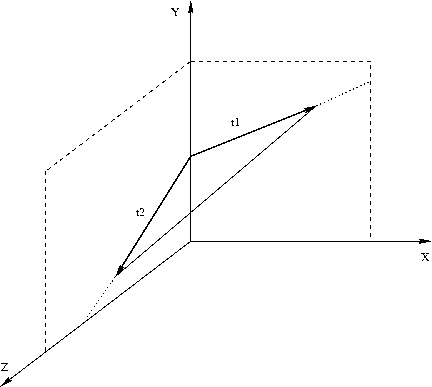
soit : t1 = N ^ Y = (n1, n2, n3) ^ (0, 0, 1) soit t1 = (1, -n1/n2, 0)
De même, t2 = (0, 1, -n2/n3)
Calcul du vecteur vitesse
Une fois t1 et t2 calculés, on en déduit V = Vx dy/dx + Vz dy/dz soit V = Vx t1 + Vz t2. Or l’évolution de la vitesse est telle que V’ = V + µA soit :
Vx’ t1’ + Vz’ t2’ = Vx t1 + Vz t2 + µ F/m + k (N + N’)/2 *(I)*
avec V’ la nouvelle vitesse, V l’ancienne, µ l’intervalle de temps, F/m l’accélération, N et N’ normales et k inconnue :
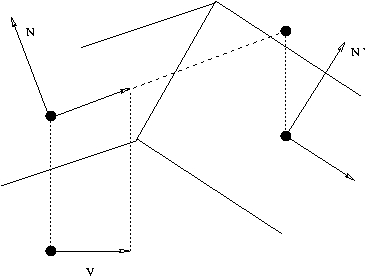
Afin d’éliminer le terme correspondant à la réaction normale (avec k inconnue) i.e la force qui fait que la bille reste en contact permanent avec la surface, on va multiplier (I) respectivement par :
Q1 = (N+N’)/2 ^ t1’
Q2 = (N+N’)/2 ^ t2’
ce qui nous donne :
V’z (Q1.t2’) = Vx Q1.t1 + Vz Q1.t2 + µ F.Q1/m d’où V’z
V’x (Q2.t1’) = Vx Q2.t1 + Vz Q2.t2 + µ F.Q2/m d’où V’x
Implantation
Initialisation : P (position initiale) et V (vitesse initiale) dont on déduit la première vitesse tangentielle (V = Vx t1 + Vz t2)
Pour chaque intervalle de temps dt (le point Pp est considéré sur une surface) :
déduire de V la nouvelle position (P’ = Pp + V dt) et projeter verticalement (P’p)
calculer la nouvelle vitesse tangentielle, pour cela :
- calculer l’accélération (A = F) par l’application des forces sans compter la réaction
- calculer la base tangentielle duale (Vz’ et Vx’) et la future vitesse 3D (V’ = V + A dt)
- projeter V’ sur le plan Q1Q2 (soit le vecteur (V’.Q1, 0, V’.Q2)) puis sur le plan tangent à la “nouvelle” surface
enfin, mettre à jour le point (P = P’) et la vitesse (V = V’)
Le projet peut être complété par des options permettant un rendu réaliste de la scène (textures, reflets, …) et/ou par l’implantation d’un éditeur de terrain.