Projet 3D - Billard
Objectifs
- à partir des éléments de MESA vus au cours des précédents TP, réaliser la modélisation d'un billard français,
- l'objet devra correspondre au modèle réel : table et pieds en bois, tapis de velour vert, lampes type suspension et queue de billard,
- l'utilisateur aura la possibilité de se déplacer autour du billard (rotation, translation, zoom) et de changer l'orientation de la queue de billard (dont la position de l'extremité est liée à celle de la boule), ceci de facon interactive par l'intermédiaire de la souris ou de touches du clavier,
- les mouvements des 3 boules devront être réaliste, c'est à dire suivre les lois de la mécanique classique mais sans tenir compte de la vitesse angulaire des boules lors des collisions.
Principes du billard français
On dispose, sur une table de 2,40, 2,80 ou 3,10 mètres, de 3 boules: une blanche toute blanche, une blanche pointée, et une rouge. Le billard français se joue généralement à deux, l'un des joueurs joue avec la blanche, tandis que l'autre joue avec la pointé. Chaque joueur doit toucher avec sa boule les deux autres boules et joue tant qu'il y parvient puis c'est au tour de l'autre joueur.
Modélisation de billard
Quelques idées de modélisation (oui, ce sont des billards américains) ...
Interaction
Elle consiste en une animation des boules en tenant compte de la vitesse angulaire, des chocs boule-boule, boule-rebord et du frottement. De plus, l'utilisateur doit avoir la possibilité de se déplacer autour de la table et de choisir l'angle de frappe de la boule par la queue de billard. Il doit aussi avoir la possibilité d'allumer ou d'éteindre chaque source lumineuse et d'activer/désactiver certaines options de rendu (texture, lumière, ...).
Rappels de mécanique
Vitesse angulaire
La rotation d'une boule sur elle-même durant son déplacement, ou vitesse angulaire, s'exprime par la relation :
Vr = -Vt/R
avec Vr : vitesse de rotation, Vt : vitesse de translation, R : rayon de la boule.
Choc élastique
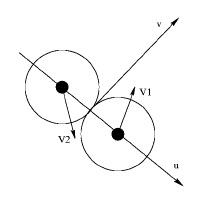
Dans le cas des boules de billard, la collision est élastique ce qui peut s'exprimer par deux lois : conservation de la quantité de mouvement et conservation de l'énergie. Les masses des boules étant supposées identiques, ces lois sont simples à mettre en equation. Soit V1, V2 les vecteurs vitesses de 2 boules et u le vecteur joignant les 2 centres de masse de 2 boules (dont on déduit v le vecteur orthogonal à u) et soit V'1, V'2 les vitesses des boules après le choc alors :
V'1 . v = V1 . v (transmission de l'impulsion suivant u)
V'2 . v = V2 . v (idem)
(V'1 + V'2) . u = (V1 + V2) . u (conservation de la quantité de mouvement, y compris suivant v mais déjà pris en compte au dessus)
(V'1)2 + (V'2)2 = (V1)2 + (V2)2 (conservation de l'énergie)
Dont on déduit la solution :
x1 = (yi2*b1*a1-yi1*b1*a1+b1^2*xi1+a1^2*xi2)/(a1^2+b1^2)
y1 = (yi2*b1^2+b1*xi2*a1-a1*xi1*b1+a1^2*yi1)/(a1^2+b1^2)
x2 = (a1^2*xi1-yi2*b1*a1+yi1*b1*a1+b1^2*xi2)/(a1^2+b1^2)
y2 = (a1*xi1*b1+yi1*b1^2-b1*xi2*a1+a1^2*yi2)/(a1^2+b1^2)
avec u[a1 b1] vecteur joignant les 2 centres de masse des 2 boules entrant en collision ; V1[xi1 yi1] et V2[xi2 yi2] les vecteurs vitesses des 2 boules avant collision ; V'1[x1 y1] et V'2[x2 y2] les vecteurs vitesses des 2 boules après collision. L'interêt de cette approche, c'est que les solutions obtenues sont directement utilisables pour définir les nouveaux vecteurs vitesses en sens et orientation.
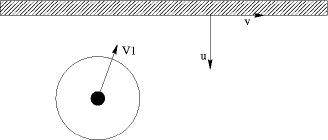
Choc non élastique
Pour prendre en compte les chocs sur les bandes (légèrement amortis), on utilisera la conservation de la vitesse tangentielle :
V.v = V'.v
et le rebond lui-même avec un coefficient de restitution c (à choisir arbitrairement entre 0 et 1) et une inversion de la vitesse :
V'.u = -c (V.u)
Frottement
Chaque boule doit avoir une vitesse nulle au bout d'un temps fini, ce qui peut s'exprimer par le fait que :
dV/dt = -f(V)
fonction qui doit s'annuler à un moment donné ; ce qui peut être exprimé par la relation :
avec k et \(\varepsilon\) choisis arbitrairement et t0 le temps au bout duquel la boule s'arrête (remarquons que l'on a donc la relation \(V_0 = k \varepsilon {t_0}^{1/\varepsilon}\) d'où \(t_0 = (V_0 / k\varepsilon)^\varepsilon\)).
Le projet peut être complété par des options permettant un rendu réaliste de la scène (texture, boules réflechissantes, ...).
Réalisation
La capture d'écran de la meilleure réalisation ci-dessous donne accès aux sources correspondantes :
